Circuit rank
The circuit rank of a graph G (also known as the cyclomatic number of G) is the minimum number r of edges to remove from the graph to make it cycle-free. It has the formula
where
- m is the number |E(G)| of edges in G,
- n is the number |V(G)| of nodes in G, and
- c is the number of connected components of G.
To actually achieve that minimum r, how careful must one be in sequentially selecting edges for removal? Although it may not be obvious, the trivial greedy algorithm that iteratively chooses any remaining cycle and deletes an arbitrary edge on that cycle does the job.
It is not too hard to see that this trivial algorithm always deletes the same number of edges from G no matter which particular edges they are. And the argument that shows this also makes clear how the formula for r arises. Consider that when the algorithm has done, the resulting graph H will still have c components and n nodes, and because H will have no cycles, each of its components will be a tree. And it is always the case that any tree T has exactly one fewer edges than nodes, or
so if we add up the versions of that equation corresponding to each component of H, we get
But |E(H)| is how many edges were left when we finished deleting edges from G, which had m edges. And the number that got deleted is merely the number we started with minus the number we ended up with, or
Homology theory
A realizable graph G is an example to 1-dimensional simplicial complex. The cyclomatic number of a graph is given by the rank of the first homology group of G with integer coefficients, i.e.
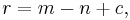
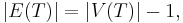
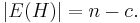
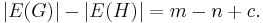
![r = \text{rank}\left[H_1(G,\Z)\right].](/2012-wikipedia_en_all_nopic_01_2012/I/ca90e7e54aca8e31b57f2d0c1c908a87.png)